El álgebra de tensores proporciona la herramienta más elegante que conozco hasta el momento para trabajar con espacios vectoriales, y en base a los principios ya vistos en las dos últimas entradas (varianza y tensor métrico) intentaremos analizar sus propiedades más importantes en esta entrada (sin entrar en muchos tecnicismos, pues por algo no soy matemático).
En venideras entradas, gracias a esta notación tan sencilla, explicaremos rápidamente la relatividad especial, extrayendo conclusiones de una forma más sencilla que con la notación vectorial.
Producto Tensorial:
El principal ejemplo de producto tensorial lo vimos en la entrada anterior para definir la métrica. Si tomamos dos vectores de un espacio de «N» grados de libertad, cada uno de ellos covariante o contravariante a elegir, y desarrollamos todos los posibles productos de sus componentes, obtenemos un tensor de dos grados de libertad, con «NxN» componentes distintas (todas las combinaciones de productos). Según la naturaleza de los vectores que hayamos usado, podremos obtener tensores covariantes, contravariantes o invariantes:
 Podemos generalizar este concepto para formar así tensores con muchos más grados de libertad, como represento en los siguientes ejemplos:
Podemos generalizar este concepto para formar así tensores con muchos más grados de libertad, como represento en los siguientes ejemplos:
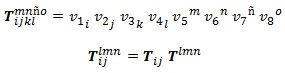 Podemos tomarnos la libertad de denominar a distintos tensores por la misma letra dentro de una ecuación tensorial si el número de indices co(contra)variantes que poseen los determina por completo. Es importante señalar de nuevo que las letras que aparecen a un lado de la ecuación tienen que volver a aparecer en el otro lado y en la misma posición (arriba o abajo), porque si no la notación se volvería inconsistente.
Podemos tomarnos la libertad de denominar a distintos tensores por la misma letra dentro de una ecuación tensorial si el número de indices co(contra)variantes que poseen los determina por completo. Es importante señalar de nuevo que las letras que aparecen a un lado de la ecuación tienen que volver a aparecer en el otro lado y en la misma posición (arriba o abajo), porque si no la notación se volvería inconsistente.
A través del producto tensorial de tensores podemos, en definitiva, crear nuevos tensores con más grados de libertad de los que lo componen (en concreto la suma de los grados de libertad de los anteriores).
No obstante, cuando el número de grados de libertad de un tensor excede de 2, pasa a ser imposible representarlo sencillamente sobre el papel, por lo que en general tensores de orden superior son poco deseables, salvo para hacer cuentas.
Rango y Dimensión:
Denominamos rango de un tensor «r», intuitivamente, al número de grados de libertad que posee, y dimensión «N» a la dimensión del espacio vectorial sobre el cual se asienta. De este modo, el número de componentes distintas de un tensor «n0» es el número de combinaciones posibles que se puede hacer con su rando y su dimensión. Por combinatoria:
 Para los físicos y los matemáticos, es importante darles significado a los tensores según su rango y su dimensión. Algebraicamente:
Para los físicos y los matemáticos, es importante darles significado a los tensores según su rango y su dimensión. Algebraicamente:
- Los tensores de rango 0 son escalares, pues tienen una única componente.
- Los tensores de rango 1 son vectores, pues tienen un único grado de libertad y «N» componentes.
- Los tensores de rango 2 son matrices cuadradas, debido a sus dos grados de libertad y a sus «NxN» componentes.
Asimismo, cada una de las componentes de un tensor puede estar parametrizada según «n» variables, de modo que, además de los grados de libertad o rango del tensor, existen los grados de libertad de sus componentes, según las cuales, por ejemplo:
- Tensores de rango 0 con 0 grados de libertad en sus componentes: pueden representar escalares.
- Tensores de rango 1 con 0 grados de libertad en sus componentes: pueden representar vectores.
- Tensores de rango 1 con 1 grados de libertad en sus componentes: pueden representar curvas en el espacio y sus métricas.
- Tensores de rango 1 con 2 grados de libertad en sus componentes: pueden representar superficies en el espacio.
- Tensores de rango 1 con 3 grados de libertad en sus componentes: pueden representar volúmenes en el espacio.
- Tensores de rango 1 con «N-1» grados de libertad en sus componentes: pueden representar hiperplanos en el espacio.
- Tensores de rango 1 con N grados de libertad en sus componentes: pueden representar elementos de N dimensiones en el espacio.
- Tensores de rango 2 con 0 grados de libertad en sus componentes: pueden representar matrices cuadradas.
- Tensores de rango 2 con 2 grados de libertad en sus componentes: pueden representar métricas de superficies.
- Tensores de rango N con N grados de libertad en sus componentes: pueden representar métricas de elementos de N dimensiones en el espacio.
*Si es necesario profundizar más en esto, hacédmelo saber en un comentario, pero buenos ejemplos al respecto son la teoría de curvas y superficies ya analizadas en este blog.
Clasificación Variante:
Si nos fijamos en la construcción de tensores a través de productos tensoriales, salta a la vista que el rango, la dimensión y el número de grados de libertad de su parametrización no son suficientes para clasificarlo completamente. Decimos que un tensor es «p» veces covariante y «q» veces contravariante (tensor p-q) según el número de componentes que posea de cada tipo. El rango del tensor, lógicamente, será la suma de la cantidad de ambas componentes. En los ejemplos que pusimos al principio vimos, por orden, un tensor 2-0, un tensor 0-2, dos tensores 1-1, un tensor 4-4 y un tensor 2-3.
Transformaciones:
Los tensores se transforman componente a componente según vimos en la entrada sobre la varianza, por lo que es fácil generalizar el concepto a un tensor p-q del siguiente modo:
Así pues, dado que las transformaciones lineales de coordenadas se representan por tensores de rango 2 (matrices), podemos decir que un tensor p-q se transforma con «p» tensores de transformación covariantes y «q» tensores de transformación contravariantes. Concretamente, en el caso de un tensor 1-1:
, o en forma matricial:
Simetrizador:
Decimos que un tensor es simétrico en algunas de sus componentes si podemos intercambiarlas obteniendo el mismo resultado. Un claro ejemplo de ello es el tensor métrico. Para indicar que un conjunto de componentes son simétricas las rodeamos de un paréntesis. Pongamos por caso un tensor 3-0 de dimensión 3:
, donde hemos escrito todas las posibles combinaciones de los números 1, 2 y 3.
Si queremos simetrizar un determinado conjunto de componentes de un tensor, lo habitual es, para cada combinación de números, sumar todas las posibles combinaciones, y hacer la media aritmética de las mismas. Tomemos por caso el tensor:
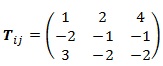 Si lo simetrizamos, sus componentes serán:
Si lo simetrizamos, sus componentes serán:
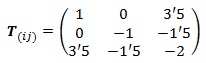 En esta nueva versión del tensor, todas las componentes son simétricas respecto a la diagonal, tal y como en principio esperábamos que sucediese.
En esta nueva versión del tensor, todas las componentes son simétricas respecto a la diagonal, tal y como en principio esperábamos que sucediese.
Si nos fijamos, al simetrizar nuestro tensor de 9 componentes hemos hecho que realmente sólo 6 componentes sigan siendo independientes.
Supongamos un tensor de rango «3» y de dimensión «3», sus combinaciones independientes serán: 111, 112, 113, 122, 123, 133, 222, 223, 233 y 333. Cualquier otra combinación de los 3 números estará repetida. Si nos fijamos, para garantizar que no repetimos ninguna combinación de índices nos podemos ir asegurando de que a medida que avanzamos hacia la derecha los números pueden ser iguales o mayores, pero nunca menores. Así pues, el número de combinaciones para un tensor simétrico de rango «r» y dimensión «N» será la suma acumulada de posibles combinaciones de cada índice del tensor, bajo la condición de no ser menor que el anterior:
 , cuyos valores según «r» y «N» son análogos al número combinatorio:
, cuyos valores según «r» y «N» son análogos al número combinatorio:
Decimos que un tensor es antisimétricos en algunas de sus componentes si al intercambiar dos de ellas el tensor cambia de signo, al cambiar dos de ellas de nuevo lo recupera, y así indefinidamente. Por ahora no hemos visto ningún tensor de estas características, pero en futuras entradas veremos ejemplos de esto como el símbolo de Levi-Civita o el tensor de campo electromagnético de Maxwell. Para indicar que un conjunto de componentes son antisimétricas las rodeamos con un corchete, y de nuevo, pongamos por caso un tensor 3-0 de dimensión 3:
Si ahora queremos antisimetrizar un determinado conjunto de componentes de un tensor determinado el método consiste en, para cada combinación de números, sumar todas las posibles combinaciones cambiando de signo según el criterio visto anteriormente, y hacer la media aritmética de las mismas. Tomemos por caso el tensor del apartado anterior por comodidad. Si lo antisimetrizamos, sus componentes serán:
, lo que expresamos como:
En esta nueva versión del tensor, podemos observar que todas las componentes cambian de signo con respecto a la diagonal por definición de la antisimetría, y que la propia diagonal es idénticamente nula, debido a que sus elementos tienen que ser iguales a sus opuestos.
En esta ocasión, al antisimetrizar nuestro tensor de 9 componentes hemos hecho que realmente sólo 3 componentes sigan siendo independientes, porque en esta ocasión los elementos de la diagonal siempre son nulos.
Supongamos de nuevo un tensor de rango «3» y de dimensión «3», su combinación independiente será ahora únicamente la 123. Cualquier otra combinación de los 3 números estará repetida, será nula, o estará relacionada con la 123 por medio de las relaciones de signos antes vistas. Si nos fijamos, para garantizar que no repetimos ninguna combinación de índices independiente nos podemos ir asegurando de que a medida que avanzamos hacia la derecha los números tienen que ser estrictamente mayores (de ahí que sólo exista esta combinación), y nunca menores o iguales. Así pues, el número de combinaciones para un tensor simétrico de rango «r» y dimensión «N» será la suma acumulada de posibles combinaciones de cada índice del tensor, bajo la condición de ser mayor que el anterior:
, cuyos valores según «r» y «N» son análogos al número combinatorio:
Una operación muy interesante (sobre todo para demostrar que ciertas magnitudes son escalares) es la contracción de índices de un tensor.
Dado un tensor p-q, podemos, en base a la notación de Einstein, igualar uno de sus índices simétricos con otro de sus índices antisimétricos, de modo que ambos desaparecen y el tensor para a ser del tipo (p-1)-(q-1). La contracción de índices es un proceso que podemos aplicar tantas veces como queramos, de forma que si tenemos un tensor p-p (de rango 2p) y lo contraemos «p» veces, obtendremos un escalar de rango 0. Como ejemplo de aplicación de las contracciones, demostraremos que la suma de los elementos de la diagonal de un tensor 1-1 es invariante frentre a transformaciones de coordenadas, o dicho en otras palabras, la invarianza de la traza.
Traza:
Volvamos al principio de la entrada. Supongamos que genero un tensor invariante 1-1 a partir del producto tensorial de un vector covariante y uno contravariante:
 Supongamos también que ahora quiero contraer sus dos índices, lo que en notación de Einstein equivale a sumar todos los elementos de la diagonal o calcular la traza:
Supongamos también que ahora quiero contraer sus dos índices, lo que en notación de Einstein equivale a sumar todos los elementos de la diagonal o calcular la traza:
 , que es un número y además un escalar, pues podemos demostrar su invarianza frente a cambios de coordenadas:
, que es un número y además un escalar, pues podemos demostrar su invarianza frente a cambios de coordenadas:
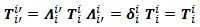 Y es que si recordamos la entrada anterior, la invarianza de la traza es evidente, pues un tensor 1-1 es el producto tensorial de un vector 1-0 con un vector 0-1, y si los íncides de estos vectores se igualaban estábamos representando el producto escalar de los mismos, un invariante.
Y es que si recordamos la entrada anterior, la invarianza de la traza es evidente, pues un tensor 1-1 es el producto tensorial de un vector 1-0 con un vector 0-1, y si los íncides de estos vectores se igualaban estábamos representando el producto escalar de los mismos, un invariante.
La conclusión es la siguiente: el producto escalar de dos vectores es equivalente a la traza del producto tensorial de los mismos tras asegurarse de que los índices del tensor están en la posición correcta (en la entrada anterior vimos cómo subir y bajar índices con la métrica).
PREFACIO: ¿Acaba todo aquí?
Soy consciente de que el contenido de esta entrada, si no se domina la materia, puede haber quedado confuso. Si es así os agradecería que sugiriéseis aportes. De todos modos, en las próximas entradas pondré un montón de ejemplos de la aplicación de los tensores en el campo de la física, reescribiendo ecuaciones conocidas, para ir entrando aún más en en el formalismo de la relatividad.
Categorías:Carrera, Matemáticas







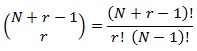
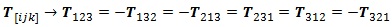

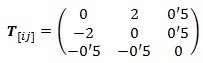
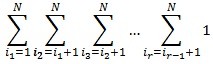
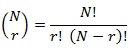
hola, soy estudiante de pedagogia en fisica y pues me ha resultado bastante complejo entender la metrica del universo de godel, me gustaria saber que tipo de conocimiento tienes con respecto a este tema, para ver si se puede compartir algun tipo de ideas. espero que te interese ahh y excelente explicacion.
Eso es relatividad general bastante avanzada y se me escapa por completo. Yo solo conozco la solución de Schwarzschild, y además acabo de publicarla recientemente. Siento no ser de más ayuda. Quizá dentro de unos meses…
Hola Adrian, gracias por tu blog. Pues que no tengo forma de entender lo que es el producto tensorial. En el mejor de los casos, x X y = xi. yj . ei X ej (X = prod tens) y yo es que me quedo “pasmao”, porque es evidente que lo que se hace es “pasar el muerto” de x, y a ei,ej.
Otras veces se habla de producto cartesiano. ¿el simple “emparejamiento” puede considerarse como una operación? ¿Qué hay detrás de todo esto?. Bourbaky y yo nunca hemos sido buenos amigos.
¿Sabes de algún libro «decente» sobre tensores?. Si no, ya podías escribir uno
Gracias y saludos
Hola, el producto tensorial simplemente es escribir como una cosa única con índices N+M la combinación de un tensor con N índices y otro con M índices. No tiene mayor interés.
Hola Adrian, vuelvo a darte la lata. A ver si me haces un buen regalo de Reyes aclarándome las ideas.
En principio un tensor de rg=2 es una transformación (multilineal si se quiere) de dos vectores que, se identifica con una matriz (en general creo que un tensor es una multimatriz ¿es así?) : yi=Tij.xj:
– ¿qué significado tiene entonces un T de rg = 3, Tijk ?¿Qué es lo que transforma y en qué?
– ¿Cuál es la transcendencia (no el concepto) de las coordenadas covariantes?
– ¿Qué papel tiene una base dual?. En principio, lo único que se me ocurre es que simplifica la expresiones al introducir la delta de Kronecker.
Saludos y gracias
Hola, si y es el transformado de x T no tiene 2 índices covariantes sino uno covariante y otro contravariante (supongo que es lo que querías poner), de modo que ahí no tienes un tensor de rango 3 sino un vector.
Otra cosa sería yijk = Tij xk, que sería un objeto nuevo sin mayor transcendencia porque no lo usas.
La gracia de las coordenadas covariantes es que se transforman todas del mismo modo y, como intuyo que no la has leído, te remito a: https://estudiarfisica.wordpress.com/2010/06/29/covarianza-contravarianza-e-invarianza-de-vectores/
Si tienes dudas aún así pregunta.
Hola de nuevo Adrián. No logro relacionar la expresión y=Tx (x,y = vectores) con Tij = xi . yj, es decir, el tensor como transformación de vectores y el tensor como producto tensorial de vectores.
Gracias.
Haces bien, porque no tienen ninguna relación :) Lo primero es la matriz que te lleva de uno al otro y lo segundo el producto de sus componentes.
No obstante, si quieres una relación inútil, tienes:
Xi = Lik Yk
Xi Yj = Lik Yk Yj = Tij
Lo que te permite expresar Tij en función de componentes de Y teniendo su matriz de transformación L para convertirlo en X.
Vale, pero se supone que los Tij son los elementos de la matriz T, y si son el producto tensorial o diádico no encajan en la ec matricial Y=TX. Entonces ¿Cuáles son los Tij?
Es que estás llamando T a 2 objetos distintos:
Xi Yj = Tij
No es, pero ni de lejos, la misma T que:
Xi = sumaj(Tij Yj)
No te encajan porque no te tienen que encajar. Son matrices distintas y cada una se obtiene según esas expresiones teniendo las componentes de los vectores. Yo a la primera antes le llamé L.
Ahora ya sí que no sé lo que es un tensor. Me suicido, adiós mundo cruel, adiós Adian :)
Ultimo intento antes del suicidio. Al menos hay que reconocer que hay una aparente contradicción. Insisto, si todo T es el producto tensorial de 2 (o más) vectores, Tij=XiYjeij, y T,en Y=TX, es un T de rg=2 (es la matriz de la transformación lineal que tú llamas L), los elementos de T deberían poder expresarse como Tij=XiYjeij, pero esto no es posible ¿Entonces?. Estírate un poco, anda; en tus manos está el que siga con vida o no :)
Ah, vale. Ahora entiendo tu duda. Quédate con este teorema «No todo tensor de rango R se puede descomponer en el producto tensorial de dos tensores de rangos N+M=R.» Que es cierto ya lo has demostrado por reducción al absurdo :)
¡Ajá! Ahora lo entiendo. El teorema que dices es el teorema de incompletitud de Gödel, que dice que hay tensores que no son tensores pero que realmente son tensores. Te estiras menos que un chicle de madera. Te lo advierto, o me lo aclaras o me tiro por la ventana (siempre y cuando debajo haya una rubia) y tú tendrás la culpa :)
A ver, si tienes una transformación lineal Lij, un tensor es cualquier objeto tal que: T’i’j’k’l’…=Li’i Lj’j Lk’k Ll’l … Tijkl…
En el caso particular de rango 1 T=Xi tienes X’i’=Li’i Xi
En el caso particular de rango 2 T=Tij tienes T’i’j’=Li’i Lj’j Tij
XiXj es, por construcción, un tensor de rango 2, pero no todos los tensores de rango 2 tienen que ser el producto tensorial de tensores de rango 1 para cumplirla.
Si Tij = Xi Xj, con Xi, Xj tensores, Tij es un tensor.
Pero eso no implica que si Tij es un tensor, entonces Tij = XiXj. De hecho esto último es falso, y es lo que tú estás suponiendo cierto. La demostración de que es falso es que, en efecto, no encuentras la relación que quieres.